Branching theorem
In mathematics, the branching theorem is a theorem about Riemann surfaces. Intuitively, it states that every non-constant holomorphic function is locally a polynomial.
Statement of the theorem
Let  and
and  be Riemann surfaces, and let
be Riemann surfaces, and let 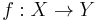 be a non-constant holomorphic map. Fix a point
be a non-constant holomorphic map. Fix a point 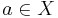 and set
and set 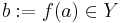 . Then there exist
. Then there exist  and charts
and charts 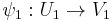 on
on  and
and 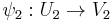 on
on  such that
such that
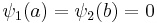 ; and
; and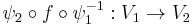 is
is 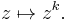
This theorem gives rise to several definitions:
- We call
 the multiplicity of
the multiplicity of  at
at  . Some authors denote this
. Some authors denote this 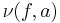 .
. - If
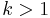 , the point
, the point  is called a branch point of
is called a branch point of  .
. - If
 has no branch points, it is called unbranched. See also unramified morphism.
has no branch points, it is called unbranched. See also unramified morphism.
References
- Ahlfors, Lars (1953), Complex analysis (3rd ed.), McGraw Hill (published 1979), ISBN 0-07-000657-1.